So I came across an interesting problem and the problem was essentially a modification of permutation problems that I had seen before. I did end up writing the brute force solution which was not good enough and had to revisit the problem for optimizing it.
Here is my best attempt at describing the problem -
Each token in a line is sent through a encryption module and gives out a transformed version of the token. The encryption module has some bugs in it and hence not all words may always get encrypted/transformed, find all possible representations of the same line so that the representations cover all possible permutations if each token was successfully transformed or not.

I hope I did not make the problem statement too confusing but to make things a bit more clearer, here is an example :-
Line -> “W1 W2"
“W1" transforms to a transformed word called “TW1”
“W2” transforms to a transformed word called “TW2”

Hence, considering that both words may not always get transformed, here are all the possible permutations of the above line.
Permutation1 -> “W1 W2”
Permutation2 -> “TW1 W2”
Permutation3 -> "W1 TW2”
Permutation4 -> “TW1 TW2”

Similarly, if the line was “W1 W2 W3” with the respective transforms being “TW1”, “TW2” and “TW3” then the possible permutations are :-
“W1 W2 W3”
“TW1 W2 W3”
“TW1 W2 TW3”
“TW1 TW2 W3"
“W1 W2 TW3"
“W1 TW2 W3"
“W1 TW2 TW3"
“TW1 TW2 TW3”

Solution 1(Brute force) :- This was the first approach I took to get things done.
Create a hashset or a treeset of results and go over each possible combination with the given token at hand. To top it off, I made the solution worse by making it recursive. So for example, if you take the first token in a three token line, then get all the possible combinations of the remaining two tokens and append them to W1 and TW1. Then, move onto W2, and get all possible permutations of (W1, TW1) and (W3,TW3) and attach them around W2 and TW2.
As can be seen, this solution is tedious and wasteful. We end up recalculating many of the already finished permutations and there needs to be an easy way to avoid that.
The worst case is when you have many tokens around the token at hand and one has to recursively calculate the combinations on both sides of the token and then again permutate with the given token. So, one creates three subproblems :-
i) Calculate permutation before the token(P1)
ii) Calculate permutation after the token(P2)
iii) Add in Permutations of P1,token,P2

I wish not to rewrite code for such a lame approach though the time complexity will be O(N X Maximum Number of Permutations before a token X Maximum Number of Permutations after a token) where N is number of tokens
which basically amounts to O(N!(N-1)!….1!).
Enough said about how bad it was.
Unfortunately, this method only worked until like 10 or 11 tokens on my laptop and my laptop gave up after that.

Solution 2(Use a tree/graph approach):-
This solution was thought about it so as to avoid recalculating a path already taken. Once all possible paths of a tree are taken, one can be assured that all possible permutations have been calculated. The way of thinking about this solution is to go have a directed graph with two start points W1 and TW1. And then do a Depth First Search for last token and its transform(in this case W3 and TW3). I think of this as a problem having two sources(W1and TW1) and two sinks(W3 and TW3).
Here is a diagram to explain the same.

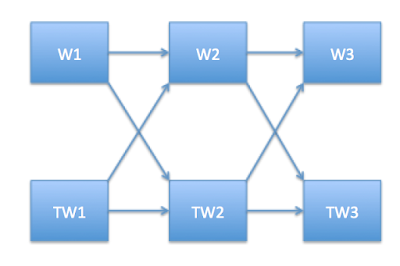fig - Graph Approach

The interesting part is that using this approach, I ended up using a little more space than I normally would to keep tabs of the nodes I have already visited.
This approach had O(V * E) time complexity which is O(N x 2N) which is essentially O(N^2) with O(2N) space complexity to maintain the visited nodes.

Solution 3(Using a binary bit based approach) :-
Thanks to Randy Gobbel for noting a pattern from the above graph and suggesting a uniquely simple approach without any extra space needed. Randy noted that each place in the resultant permutation has two possible values(W or TW). This is more or less like 0 or 1. Hence, the permutations amount for a three token line amount to -
000, 001, 010, 011, 100, 101, 110, 111
where 0 -> the token itself
          1 -> the token’s transform
As a result, this solution boils down to simply iterating over all possible values from 0 to 2 raised to the power of the number of tokens. Below is the code for the approach. The method signature involves a list of tokens and a Map/Dict containing transforms for each token.

1:  public List getPossiblePermutations3(List words, Map transformMap) { 
2:        if (words == null || words.isEmpty()) 
3:            return null; 
4:        List permutationList = new ArrayList<>(); 
5:        for (int i = 0; i < (int)Math.pow(2,words.size()); ++i) { 
6:            StringBuilder permutation = new StringBuilder(); 
7:            for (int j = 0; j < words.size(); ++j) { 
8:                //Check if bit is set 
9:                if((i & (int)Math.pow(2, j)) == 0) 
10:                    permutation.append(words.get(j) + " "); 
11:               else 
12:                    permutation.append(transformMap.get(words.get(j)) + " "); 
13:            } 
14:            //Trim out end spaces/blank characters 
15:            permutationList.add(permutation.toString().trim()); 
16:        } 
17:        return permutationList; 
18:    } 

The time complexity for this approach is O(N x 2^N) with no space implications.

Thanks for reading…